【Day 26】《實作》搭建多元線性回歸模型

15th鐵人賽機器學習模型多元線性回歸

許皓翔

團隊最強資工大電神

2023-10-11 10:47:34

467 瀏覽

分享至

前言

昨天我們做的簡單線性回歸模型，特徵數量只有一個，若現在有多個 ( 一個以上 ) 特徵，這樣的線性回歸模型就有多個自變數輸入，也就是我們今天要實作的多元線性回歸模型 ( Multiple Linear Regression )，而我們前面有提過，做為一個多元線性回歸的模型，模型的樣貌即為 $y_{pred} = w_1*x_1+w_2*x_2+w_3*x_3+b$ 的形式，這樣便能夠讓模型取得更多元的資訊並做出預測。

使用套件

本次實作會用到的套件：

import pandas as pd
import numpy as np
from sklearn.preprocessing import OneHotEncoder, StandardScaler # 用來做資料預處理
from sklearn.model_selection import train_test_split # 用來做訓練資料分割

資料集

https://drive.google.com/file/d/1ZkqE1IpTieSTrnc9kUsRukK5uoRBi91m/view?usp=drive_link

限定 numpy 陣列輸出的格式並讀取資料集 csv 檔 ( 上方連結取得 )，這個資料集內容和昨天簡單線性回歸所用的相似，只是多了幾個特徵欄位，共三個特徵欄位，分別是 YearsExperience、EducationLevel 和 City，與一個標籤欄位 Salary：

np.set_printoptions(formatter={"float": "{: .2e}".format}) # 限定輸出格式
data = pd.read_csv("Salary_Data2.csv") # 讀取資料

資料 ( 此只列出 10 筆 ) :

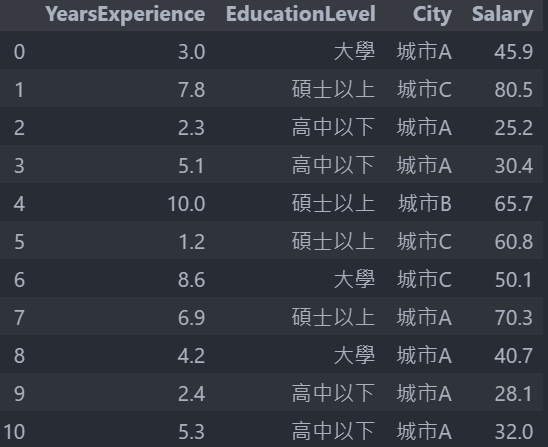
上一篇我們的 model 是用年資來預測月薪，model 的 feature 只有年資，所以就用簡單的線性回歸完成，上圖是資料，而現在我們還要考慮多個 feature，有年資、教育程度跟城市，就可用多元線性回歸來做，一開始就先暫定我們的 model 為 $y_{pred} = w_1*x_1+w_2*x_2+w_3*x_3+b$ ，但教育程度和城市並不是數字型態不能拿來與參數相乘，因此就需要做資料的預處理。

資料預處理 Preprocessing

下面要進行資料預處理的特徵編碼部分，將資料轉換為 model 可以處理的數值型態，常見的特徵編碼方式有 Label Encoding 和 OneHot Encoding：

標籤編碼 Label Encoding

在這邊用 map() 因為教育程度的高低對於薪資結果有一定影響，所以我們可將不同教育程度對應到不同的整數值 : 高中以下 → 0，大學 → 1，碩士以上 → 2，這就是 Label Encoding 技術，其處理的特徵存在著高低關係：
```
data["EducationLevel"] = data["EducationLevel"].map({"高中以下": 0, "大學": 1, "碩士以上": 2}) # Label Encoding
```
獨熱編碼 OneHot Encoding

換作是城市，這種特徵就沒什麼高低關係，城市之間都平等無優劣，此時如果要將特徵轉換為整數時，可以直接把它轉換為多個特徵，就像下圖第一列就代表 CityA，第二列代表 CityB，第三列代表 CityC，這種技術就叫做 OneHot Encoding。

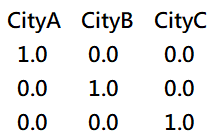
先宣告 OneHotEncoder 轉換器物件，用 fit ( ) 讓轉換器先看過資料 ( 必須要是二維 )，然後在用 transform ( ) 去轉換，轉換後會得到稀疏矩陣，再轉成陣列並加到原資料中就行了：
```
oneHot_encoder = OneHotEncoder() # 宣告轉換器物件
oneHot_encoder.fit(data[["City"]]) # 讓轉換器先看過資料
city_encoded = oneHot_encoder.transform(data[["City"]]).toarray() # 把轉換後得到的稀疏矩陣轉成陣列
data[["CityA", "CityB", "CityC"]] = city_encoded # 轉換後資料加入原本資料
```
此時資料會長這樣 :

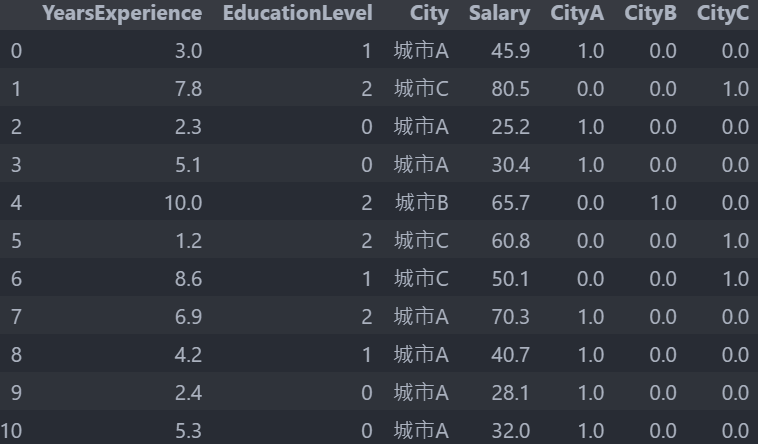
我們已經將原本文字型態的城市轉換成數字型態來表示，所以可以刪去 City 欄位了，其實我們知道其中兩個 City 的數值就可以推斷出另一個 City 的值，像是當 City A : 1.0，City B : 0.0 時，就可以推斷 CityC 是 0.0，所以我們可以刪去其中一個欄位，這邊我們選擇刪去 CityC 欄位：

data = data.drop(["City", "CityC"], axis=1) # 刪除兩個不必要的欄位

切分資料集

如果把全部的資料都拿來訓練，就沒有一筆陌生資料 ( 測試資料 ) 可以對最終模型 ( 最佳參數 ) 測試，如果是用訓練資料來做測試因為資料都已經看過了所以測出來會不準，所以通常我們會把資料切割為訓練和測試資料，就會用到 train_test_split函數來幫我們切割，這邊 20% 為測試資料 80% 為訓練資料，並且設定 random_state 確保每次執行分割資料的結果都一樣，特徵值現在有四個，因此修改我們的 model 為 $y_{pred}=w_1*x_1+w_2*x_2+w_3*x_3+w_4*x_4+b$ ：
```
x = data[["YearsExperience", "EducationLevel", "CityA", "CityB"]] # feature
y = data["Salary"] # Label
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=87) # 切割資料集
x_train = x_train.to_numpy() # 方便後續計算轉換為 numpy 格式
x_test = x_test.to_numpy() 
```
資料標準化處理

我們再對我們的訓練和測試時的特徵資料進行標準化處理，把資料數值的尺度都等比例縮小至較小的區間 ( 讓彼此數值落差較小 )，值得注意的是在做測試特徵資料正規化時，我們直接用已經擬和過的 scaler 物件呼叫 tranform() 方法，因為我們要用處理訓練特徵資料時 ( scaler.fit(x_train) ) 所學習到的平均值和標準差來處理測試特徵資料的尺度轉換：
```
scaler = StandardScaler() # 宣告 StandardScaler 物件
scaler.fit(x_train) # 對訓練特徵資料進行擬和
x_train = scaler.transform(x_train) # 訓練特徵資料尺度轉換
x_test = scaler.transform(x_test) # 測試特徵資料尺度轉換
```

成本函數

和之前成本函數的觀念一樣，先設計好 model ( y_pred ) 再求出成本，傳入的 w 是一維陣列用來與 x_train 相乘：

def cost(w, b):
    y_pred = (x_train * w).sum(axis=1) + b
    cost = ((y_train - y_pred) ** 2).mean()
    return cost

再來是定義計算梯度的函數 :

def gradient(w, b):
    y_pred = (x_train * w).sum(axis=1) + b
    w_gradient = np.zeros(x_train.shape[1])
    b_gradient = (-2 * (y_train - y_pred)).mean()
    for i in range(x_train.shape[1]):
        w_gradient[i] = (-2 * x_train[:, i] * (y_train - y_pred)).mean()
    return w_gradient, b_gradient

實作 Gradient Descent 求出最佳解 w_final、b_final ：

def gradient_descent(w_init, b_init, learning_rate, cost_func, gradient_func, run_iter, per_iter=1000):
    w = w_init
    b = b_init
    w_hist = []
    b_hist = []
    cost_hist = []
    for i in range(run_iter):
        w_gradient, b_gradient = gradient_func(w, b)
        w_step = - learning_rate * w_gradient
        b_step = - learning_rate * b_gradient
        w = w + w_step
        b = b + b_step
        w_hist.append(w)
        b_hist.append(b)
        cost_hist.append(cost_func(w, b))
        if(i % per_iter == 0):
            print(f"time{i:5}, cost:{cost_func(w, b)}, w:{w}, b:{b}")
    return w, b, w_hist, b_hist, cost_hist

# 初始參數
w_init = [1, 2, 3, 4] 
b_init = 1
# 學習率
learning_rate = 1.0e-3
# 迭代次數
run_iter = 20000

w_final, b_final, w_hist, b_hist, cost_hist = gradient_descent(w_init, b_init, learning_rate, cost, gradient, run_iter)

把有最佳參數的 model 預測結果和測試資料進行比對並做成 DataFrame，更加容易的看出預測的偏差：

y_pred = (x_test * w_final).sum(axis=1) + b_final # 把最佳參數放進 model 
pd.DataFrame({
    "y_pred": y_pred,
    "y_test": y_test
})

執行結果 :

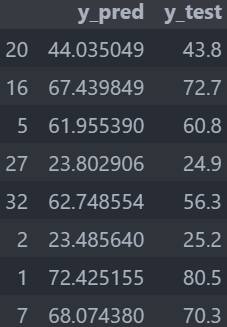
最後在算出這個最佳參數 model 的成本大小：

y_pred = (x_test * w_final).sum(axis=1) + b_final
cost = ((y_test - y_pred) ** 2).mean()

套用到真實的案例，把這個 model 寫成一個函數，傳入經過 OneHot Encoding 的測試資料 ( 二維 ) 後經過資料縮放轉換後放進最佳參數的 model 中最會得到每個傳入資料的預測值：

def model(data):
    x_real = np.array(data)
    x_real = scaler.transform(x_real) # 資料縮放正規化
    y_real = (x_real * w_final).sum(axis=1) + b_final
    return y_real
model([[5.3, 2, 1, 0],
       [7.2, 0, 0, 1]]) # 傳入二維測試資料